JZL Capital：比特币天敌? 2040 量子计算分析（1）：量子威胁时间线

比特币天敌？——这个问题如同一片阴影，笼罩在价值数万亿美元的加密资产世界之上。量子计算，这个诞生于物理学深奥理论的革命性技术，被普遍认为是目前唯一有潜力从根本上破解现代密码学的力量。比特币的安全基石——椭圆曲线数字签名算法（ECDSA）和安全哈希算法（SHA-256），在经典计算机面前几乎坚不可摧，但在理论上，它们对量子计算机的 Shor 算法和 Grover 算法却显得较为脆弱。

这柄悬于加密货币之上的达摩克利斯之剑究竟何时会落下？为了拨开迷雾，洞见未来，JZL Capital 启动“2040 量子计算”系列分析，旨在提供一份前瞻且深入的路线图。

本系列分析的第一部分《量子威胁时间线》，将给出破解比特币加密算法的技术门槛，以及目前预计的时间线。

1. 历史与概念的起源

量子计算的理论基础始于 20 世纪 70 年代末。1980 年，保罗·贝尼奥夫（Paul Benioff）发表了第一篇关于量子版图灵机的正式描述，为该领域奠定了数学和物理基础，证明了量子力学如何支撑计算 。紧随其后的是理查德·费曼（Richard Feynman）在 1981 年一次会议上的重要主题演讲，他普及了这一思想，指出要精确模拟本质上是量子的物理系统，就需要基于量子力学原理运行的计算机。他引入了“量子模拟器”的概念，尽管它无法像图灵机那样执行任何程序，但可以用于模拟量子力学现象，这篇演讲通常被认为是激发量子计算学科兴趣的开端 。

1985 年，大卫·迪奇（David Deutsch）进一步推进了这一概念，他指出图灵基于经典物理的通用计算机无法模拟量子计算机。迪奇通过使用量子力学重新构建图灵的工作，提出了“通用量子计算机”的概念，这种计算机能够模拟任何物理过程，这在理论上为量子计算的普适性奠定了基石 。

然而，尽管有这些理论突破，量子计算机在实践中的明确应用案例仍未出现。直到 1994 年，美国数学家彼得·秀尔（Peter Shor）发明了一种量子算法（Shor 算法），能够在多项式时间内解决大数分解和离散对数问题。大数分解和离散对数是许多领先加密方案（如 RSA 和比特币签名使用的 ECDSA）的基础，其难度随数字增大而呈指数级增长。秀尔算法能够以指数级速度快于任何已知经典算法解决这些问题，这引发了人们对量子计算机可能破解现代加密的担忧，并推动了后量子密码学的发展 。这一突破性算法的出现，无疑为量子计算领域注入了巨大的兴趣和活力，因为它首次展示了量子计算在解决实际问题上的潜在“杀手级应用”。

1996 年，贝尔实验室的计算机科学家洛夫·格罗弗（Lov Grover）提出了另一种重要的量子算法（Grover 算法）用于非结构化搜索。在没有明确组织系统的数据库中查找信息是一个常见的计算机科学问题，即使是最好的经典搜索算法在面对大量数据时也可能非常缓慢。格罗弗算法利用量子叠加现象，显著加快了搜索过程 。

这些理论进展很快得到了实验验证。1998 年，日本电气公司（NEC）研究员中村泰信 (Yasunobu Nakamura）和同事成功展示了对单个固态超导量子比特的相干控制。同年，由 IBM 研究员艾萨克·庄（Isaac Chuang）领导的团队首次在硬件上演示了量子算法的实现，他们成功地在两量子比特计算机上运行了格罗弗算法。三年后，庄还领导了 Shor 算法在七量子比特处理器上的首次实现。

这些里程碑事件标志着量子计算从纯粹的理论探索走向了实际的硬件实现，为后续的快速发展铺平了道路。

2. 量子计算是否能攻克比特币加密算法？

比特币依赖两种核心加密算法： SHA-256（安全哈希算法）和ECDSA-256（椭圆曲线数字签名算法），经典计算机几乎无法破解它们，但是善于破解加密信息的量子计算机呢？

SHA-256：挖矿与地址生成的核心算法

SHA-256 是比特币工作量证明（PoW）挖矿的核心算法，用于计算区块哈希。矿工通过寻找满足特定条件的哈希值（即哈希值小于网络目标值）竞争记账权。此外，SHA-256 还用于从公钥生成比特币地址（公钥经 SHA-256 和 RIPEMD-160 哈希后生成地址）。在经典计算中，SHA-256 的预映像攻击需要 O(2^256) 次操作，挖矿则需要 O(D × 2^32) 次操作，其中 ( D ) 是网络难度。

量子计算机对 SHA-256 的威胁：Grover 算法

量子计算机通过 Grover 算法 可将无结构搜索问题的复杂度从 ( O(N) ) 降低到 O(SQRT(N))，提供二次加速。对于比特币挖矿，搜索空间大小由难度 ( D ) 决定。当前比特币网络难度约为 D ≈ 1.17 × 10^14 ( 约 2^46.73)，经典计算机挖矿需要约 O(1.17 × 10^14) 次哈希计算。

而 Grover 算法将复杂度降低到：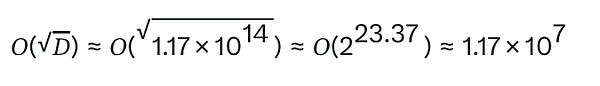

即约 1,170 万次量子操作，理论上将挖矿所需计算量减少约 1,170 万倍。这使得量子计算机能够更快找到有效哈希，加速 PoW 挖矿并提高获取区块奖励的效率。

早期量子计算机实际限制

尽管 Grover 算法显著降低计算量，但目前量子计算机量子门操作速度普遍较慢，最快也是在 10-20 纳秒级别（换算为频率约 100MHz-200MHz)，导致计算次数相比经典计算机要少的多。即使早期量子计算机达到了能够运行 Grover 算法的最低标准，其实际挖矿能力可能不如一台未来的顶级 ASIC 矿机。

而要达到对比特币算力的霸权，则需要一台能在十分钟内完成全部 1.17 × 10^7 次操作的量子计算机，否则无法和全球的 ASIC 矿机竞争。并且随着比特币网络难度的提升，所需的计算能力也随之提升。如果量子计算机能达到这种性能，则可以实施 51% 攻击，导致：

1. 双花攻击（重复花费同一笔资金）。

2. 阻止某些交易被确认。

3. 重组近期区块链历史（长期历史因难度累积难以篡改）。

ECDSA：

比特币使用 ECDSA（基于 secp256k1 椭圆曲线，256 位）生成公私钥对和数字签名，用于验证交易的合法性。私钥持有者通过签名授权交易，而公钥和地址保护资金安全。ECDSA 的安全性依赖于椭圆曲线离散对数问题（ECDLP），即使是目前最强的经典计算机也几乎不可能破解。

但量子计算机通过 Shor 算法可以在多项式时间内破解 ECDLP，从而从公钥推导出私钥。如果量子计算机达到足够规模，攻击者可能破解暴露公钥的地址，伪造签名并窃取资金。若 ECDSA 被破解，暴露公钥的地址将失去保护，虽然这不会直接导致整个比特币网络崩溃，但会影响特定地址的安全（比如中本聪地址）。

量子计算破解的技术门槛：

量子计算需要逻辑量子比特（logical qubits）来执行可靠计算，而每个逻辑比特需要通过量子纠错码由数百至数千个物理量子比特（physical qubits）构造。

• 当前估计，想要通过 Grover 算法运行 SHA-256，需要约 1000-1500 个逻辑比特，相当于需要百万至数百万个物理比特。而根据比特币挖矿公司 AMINA 的一篇相关文章，要获得足以实施 51% 攻击的算力，则需要大约 10 亿个物理比特。

• 破解 ECDSA（通过 Shor 算法）需要约 2500-3000 个逻辑比特，相当于数百万至千万个物理比特。

这些数字基于当前纠错技术（如表面码），实际需要的物理比特可能因硬件进步而减少。此外，运行 Shor 或 Grover 算法需要极低的错误率和大量量子门操作（例如，Shor 算法需约 10^9 次 T 门），对量子计算机性能要求极高。

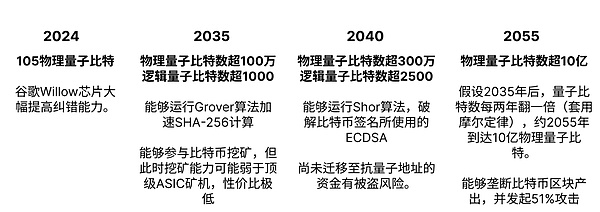
然而，目前最先进的量子芯片之一的谷歌的 Willow 仅有 105 个物理量子比特，其最大的突破是将超导量子比特的纠错能力显著提高。但这 105 个物理量子比特仅能支持一个逻辑比特，并且这个逻辑比特的错误较高且持续时间短。

相比破解 ECDSA 或 SHA-256 所需的千级逻辑比特，当前技术差距仍然巨大。谷歌量子在其里程碑路线图中显示，他们希望在第三里程碑阶段构建一个能够持久延续的逻辑量子比特，在第四个里程碑达到上万个物理比特，并建立两个逻辑量子比特的协同运作。而到第六个里程碑才能达到 100 万个物理比特和上千个逻辑量子比特协同运作。而谷歌预计，他们可能需要 10 到 20 年以上的时间才能实现第六个里程碑，也就是 2035 至 2045 年。IBM 的预计则更为乐观，给出了在 2033 年达到 2000 个逻辑比特的目标。

折中 IBM 和谷歌的预期，我们认为，比特币目前的两种算法最快将在 2040 年被量子计算机攻破。

以下是几个关键时间点：

3. 比特币的抗量子应对措施

尽管目前来看，量子计算距离攻破比特币加密算法仍然较为遥远，但若不采取措施，这一天终将到来。特别是像中本聪这样持有大量比特币，并且已经暴露公钥的早期地址，风险尤为突出。但比特币的算法并非一成不变，而是可以在矿工的支持下，通过软分叉或硬分叉升级抗量子能力。

比特币的抗量子安全依赖于替换或增强当前的加密算法，以抵御量子计算的威胁。以下是主要的技术方向：

增强 PoW 机制

• 调整 PoW 难度：增加挖矿算法的复杂性，例如引入更长的哈希函数（如 SHA-512）或组合多种哈希算法，以提高量子破解的难度。

• 抗量子 PoW 算法：研究新的 PoW 机制，如基于抗量子问题的算法。例如 Momentum PoW，量子加速仅为 T^2/3，优于现有 PoW 的 T^1/2。而基于格问题的 PoW 可以以完全抵御 Grover 算法的加速。

• 混合 PoW：在过渡期内，结合 SHA-256 和抗量子 PoW 算法，确保网络在量子威胁出现前逐步升级。

抗量子签名算法

比特币的 ECDSA-256 依赖椭圆曲线离散对数问题（ECDLP），在量子计算机运行 Shor 算法时易被破解。为此，社区正在研究抗量子签名算法，包括：

• 基于哈希的签名：如 XMSS，量子安全级别为经典安全级别一半，具可证明安全性。

• 后量子密码算法：NIST 标准化算法如 Dilithium（量子安全 125 位，签名 + 公钥长度较短），避免易受侧信道攻击的 BLISS。

• 实施方式：抗量子签名可通过软分叉引入新的脚本类型（如新的 OP_CODE）或硬分叉修改比特币协议，生成抗量子地址。软分叉更具兼容性，允许旧节点继续运行，但新地址将获得量子抗性保护。

地址格式升级

当前的 P2PK（支付到公钥）和 P2PKH（支付到公钥哈希）地址在量子计算机面前较为脆弱，尤其是暴露公钥的地址。未来的新地址可能采用抗量子哈希函数或签名方案，但这需要持有者将比特币转移至新地址才能生效。

但地址格式升级仍然无法保护中本聪的地址，假如中本聪不将比特币从旧地址中转移到抗量子地址的话，仍然有被窃取的可能。中本聪的各个早期地址（共持有约 100 万枚比特币）多为 P2PK 格式，在交易后直接暴露公钥而不是哈希，量子威胁下极易被攻击。中本聪地址以及其他远古地址可能成为量子时代的 ”海贼王大秘宝”，而其资金被盗会引发加密市场的剧烈波动。目前较为可行的办法是通过一次分叉将这些沉寂的远古地址冻结，但这将违背比特币的去中心化和私有财产不可侵犯的理念，因此争议较大。尽管如此，在利益的驱动下大多数矿工都会同意这个方案。

结论

量子计算正从理论走向现实，其对现有加密体系的颠覆性潜力，尤其是对比特币等加密货币的威胁，已成为科技界和金融界关注的焦点。对于比特币而言，量子威胁确实存在，但并非迫在眉睫。而相比 Grover 算法的加速挖矿，Shor 算法破解比特币钱包导致的威胁更为显著。

然而，构建一台足以执行这些攻击的量子计算机，需要数千级别高质量逻辑量子比特和百万级别物理量子比特，我们预计这大概需要在2040 年以后才能实现。

比特币社区拥有充足的时间窗口来部署应对策略，即通过分叉升级到后量子密码算法，并将资产转移至抗量子标准的钱包中。真正的考验或许在于如何处理像中本聪地址这类无法主动迁移的“远古资产”，这不仅是技术问题，更是对比特币去中心化和“代码即法律”理念的挑战。

在本系列的下一章中，我们将更深入了解量子计算的概念，以及多个目前主流和有潜力的量子计算技术路径。

本文仅供研究学习，不构成投资建议。

作者：Steven, 加州大学伯克利分校经济学学士、约翰霍普金斯大学金融硕士，现任 JZL Capital 衍生品策略研究员